Bayesian inference is a statistical method based on Bayes’ theorem, in which the probability of a hypothesis is updated based on prior evidence and a model created to explain the data (Konigsberg and Frankenberg 2013). In Bayesian inference probability is treated as “conditional probability”, the probability of an outcome given another outcome (Casella 2008; Puga et al. 2015b). At the core of Bayesian inference is Bayes’ theorem (Puga et al. 2015a), in which the probability of a model M given the data D is described by P(MǀD), and it is calculated as follows:

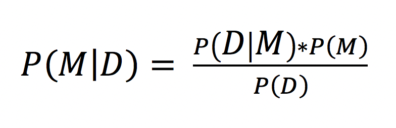
Here, P(DǀM) is referred to as the likelihood, and it describes the compatibility of the data, given a model (specifically, it is the probability of the model M producing the data D). The P(M) is the probability of the model M before the data D are observed, also known as the prior probability or simply a prior. A prior represents our degree of belief in the values that a parameter can take, and it modifies the likelihood to produce the probability of a model given the data P(MǀD). The P(MǀD) is referred to as the posterior probability. Finally, P(D) represents the probability of the data. Critically, when posterior probabilities are calculated using the same data, P(D) takes the same value in all independent calculations (as the empirical data are the same for all), it is therefore a fixed scalar of P(MǀD) and is often ignored:

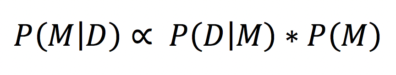
Model testing in Bayesian frameworks are relatively straightforward and is usually performed using Bayes factors. A Bayes factor is the ratio of the prior odds of two hypotheses (i.e., the odds of model M₁ over model M₂) to the posterior odds of the hypotheses (Kass and Raftery 1995). The Bayes factor K is thus the ratio of the two marginal likelihoods of the models:

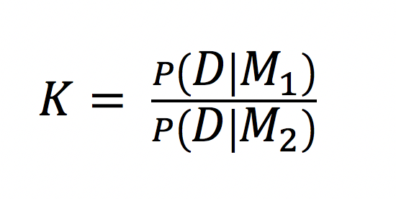
Conveniently, Kass and Raftery (1995) provide a scale to discriminate between models based on the value of the ratio K.  Notably, though this scale has assumed some authority in the field of Bayesian inference, it is itself a suggestion when interpreting the importance of Bayes factor values (as are schemes regarding the significance of p­-values). It is also important to remember when calculating Bayes factors that most coalescent or phylogenetic software packages report probabilities and likelihoods in log_e units (this is done because likelihoods of phylogenies and genealogies can be exceeding small).