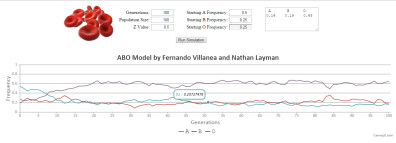
ABO-NX MODEL (beta version)

ABO-NX is a simple mathematical model which simulates the interaction between balancing selection and genetic drift as it shaped the frequency composition of the ABO locus in modern humans, as described in Villanea et al. 2015. ABO-NX is meant to be used as a free teaching tool, where students can modify the starting frequencies of the A, B, and O alleles in a population, as well as the strength of balancing selection (Z), the starting population size, and the number of generations for which the model tracks the change in allele frequencies over time.

CONTROLS:

Generations: The number of iterations ABO-NX will run. A human generation is equivalent to roughly 30 years.

Population Size: The number of gametes times 2 produced every generation. The strength of genetic drift is inversely proportional to this number.

Z Value: The strength of balancing selection. The strength of selection z is approximately ten times s; the difference in absolute fitness between genotypes.

Starting A Frequency: A value between 1 and 0. The global population average frequency of the A allele is 0.240.

Starting B Frequency: A value between 1 and 0. The global population average frequency of the B allele is 0.133 .

Starting O Frequency: A value between 1 and 0. The global population average frequency of the O allele is 0.627.

|Go to ABO-NX|

BACKGROUND

The maintenance of genetic variation has important consequences because heritable genetic variation fuels the evolutionary process. Balancing selection is of particular interest because it can produce stable genetic polymorphic systems (Crow and Kimura 1970). Examples of strong balancing selection are particularly compelling, as such a mode of selection can have profound impacts on patterns of genetic diversity across the genome (Charlesworth 2006). Balancing selection has also been proposed to explain high genetic variability and the evolutionary stability of several polymorphisms in vertebrates, most notably the major histocompatibility complex (MHC) (Hedrick and Thomson 1983; Hedrick 1994; Hedrick 2002), opsin, and the ABO blood groups of humans.

The ABO locus is one of the better studied genetic systems in humans. The ABO gene codes for a glycosyltransferase which modifies a precursor antigen into the A or B antigens. The O antigen results from a glycosyltransferase, which lacks enzymatic function. Human host antibodies are tolerant of self-produced ABO antigens, but agglutinate against foreign forms; thus, ABO phenotypes must be correctly identified to ensure successful blood transfusions. The maintenance of a class of O alleles with lost glycosyltransferase activity over such a long evolutionary time is consistent with a form of asymmetric negative frequency dependent selection (NFDS) where the O allele has some advantage over the A and B alleles.

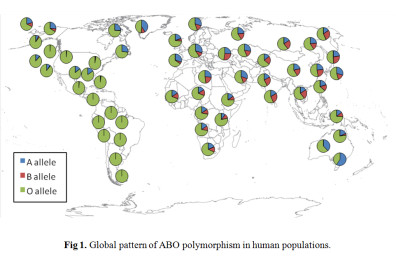
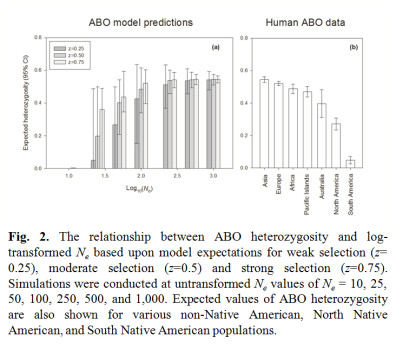
The ABO locus in humans is characterized by elevated heterozygosity and very similar allele frequencies among populations scattered across the globe (Fig. 1). Using knowledge of ABO protein function, we developed ABO-NX, a simple model of asymmetric negative frequency dependent selection and genetic drift to explain the maintenance of ABO polymorphism and its loss in human populations. In ABO-NX, regardless of the strength of selection, models with large effective population sizes result in ABO allele frequencies that closely match those observed in most continental populations (Figure 2). Populations must be moderately small to fall out of equilibrium and lose either the A or B allele (N_e ≤ 50) and much smaller (N_e ≤ 25) for the complete loss of diversity, which nearly always involved the fixation of the O allele. A pattern of low heterozygosity at the ABO locus where loss of polymorphism occurs in our model is consistent with small populations, such as Native American populations.

THE MODEL

We considered human populations where NFDS occurs in the zygote phase and was determined by ABO genotype. We modeled ABO locus evolution as a deterministic outcome of natural selection. our model uses general equations for frequency dependent natural selection. Our model is built under the assumption that a human host generates antibodies that recognize foreign antigens. Fitness of an individual host phenotype depends on its ability to recognize pathogens based exclusively on the ABO antigen-antibody system. Pathogens which infected a host of a specific phenotype the previous generation are considered to have evolved to better infect hosts presenting the same cell membrane antigens; thus, the fitness of a host genotype is diminished by the presence of other host genotypes which express the same antigen phenotype. The fitness of particular host genotypes is a negative function of the frequency (f) of genotypes expressing the same antigen phenotype:

The A, B, and O alleles of the ABO gene code for transferases, which collectively determine a host phenotype by modifying the H antigen into A and B antigens, and in the instance of O, a defective transferase which does not modify the H antigen. O heterozygotes are recessive and AB heterozygotes are co-dominant. Because the A and B alleles code for an enzyme with “trans” function, the A and B alleles are completely dominant over the O allele, as heterozygotes would still produce one functional copy of the glycosyltransferase enzyme, which would in turn convert all H antigens into A or B antigens. Thus, homozygotes and heterozygotes for A or B phenotypes are treated equally in terms of fitness.

The strength of selection acting on the ABO locus should vary, depending upon the environment. We controlled the strength of selection exerted by pathogens in this model using a tuning parameter, (z) that ranges from 0 (neutrality) to 1 (very strong natural selection). In biological terms, (z) may account for incomplete transmission of pathogens between hosts, other components of the immune system overcoming infection, or a delay between infection and mortality. As an important note, the strength of selection z is not a selection coefficient (s) as understood in classic population genetics. There is no explicit equation relating (z) and (s), but instead, we have used the equations in the model to calculate a selection coefficient for each (z) value as the difference in absolute fitness between genotypes, where s is approximately one tenth of z; therefore, “strong” selection (z = 1.0) only corresponds to a selection coefficient of s = 0.10.

A and B allele initial frequencies and selection regimes are treated as equal in order to simplify the NFDS model, which is focused on understanding the fixation of O alleles. Change in allele frequency in response to NFDS was quantified using the relative fitness of genotypes:

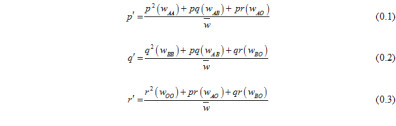
We incorporated stochastic variation in allele frequencies in accordance with the Wright-Fisher model of genetic drift. The frequency of alleles following selection (p’, q’, r’) were used as expected gamete frequencies, and a finite number of gametes equal to 2N_e were randomly sampled with replacement from this pool; random mating produced zygote frequencies.

REFERENCES

Charlesworth, D. (2006). “Balancing Selection and Its Effects on Sequences in Nearby Genome Regions.” PLoS Genet 2(4): e64.

Crow, J. F. and M. Kimura (1970). An introduction to population genetics theory. New York, Harper & Row

Hedrick, P. W. (1994). “Evolutionary Genetics of the Major Histocompatibility Complex.” Amer Nat 143(6): 945-964.

Hedrick, P. W. (2002). “Pathogen resistance and genetic variation at MHC loci.” Evolution 56(10): 1902-1908.

Hedrick, P. W. and G. Thomson (1983). “Evidence for Balancing Selection at HLA.” Genetics 104: 449-456.

Villanea, F. A., K. N. Safi, et al. (2015). “A General Model of Negative Frequency Dependent Selection Explains Global Patterns of Human ABO Polymorphism.” PLOS One 10(5): e0125003.